Binary Search Trees

25 BST

25.2 Binary Search Trees Basics

Binary Tree

• length of a path
• depth of a node
• level of the tree
• siblings
• left(right) child of the node
• leaf
• height of a nonempty tree
• height of a empty tree

BST

• no duplicate elements
• for every node in the tree , the value of its left child is less than the value of the node, and the value of its right is greater than the value of the node.

25.3 Representing Binary Search Tree

can be implemented using a linked structure

• each node contains a value and two links named left and right that reference the left and right child.

  class TreeNode<E> {
      protected E element;
      protected TreeNode<E> left;
      protected TreeNode<E> right;
  
      public TreeNode(E e) {
      element = e;
      }
  }
  

• use root to refer to the root node of the tree.

• if tree is empty, root is null

  TreeNode<Integer> root = new TreeNode<>(60);
  root.left = new TreeNode<>(55);
  root.right = new TreeNode<>(100);
  
  

25.4 Searching for an Element

• to search, START FROM THE ROOT ,and scan down from it until a match is found or arrive at an empty subtree

• repeat compare left and right with you target

  public boolean search(E e){
  
  TreeNode<E> current = root;
  while (current !=null){
      if (e < current.left) {
      current = current.left;
      }
      else if (e > current.element){
      current = current.right;
      }
      else
          reture = ture;
  }
  }
  
  

25.5 Inserting an Element into a BST

• CREATE A NODE AS ROOT ,and scan down which node can be this new node’s parent

boolean insert(E e){
if (tree is empty)

}else {
    parent = current = root ;
    while (current != null){
     if(e <the value in current.element){
     parent = current;
     current = current.left;
     }else if (e > the value in current.element){

    parent = current;
    curretn = current.right;
    }
    else
      return false
    }
    return ture
}

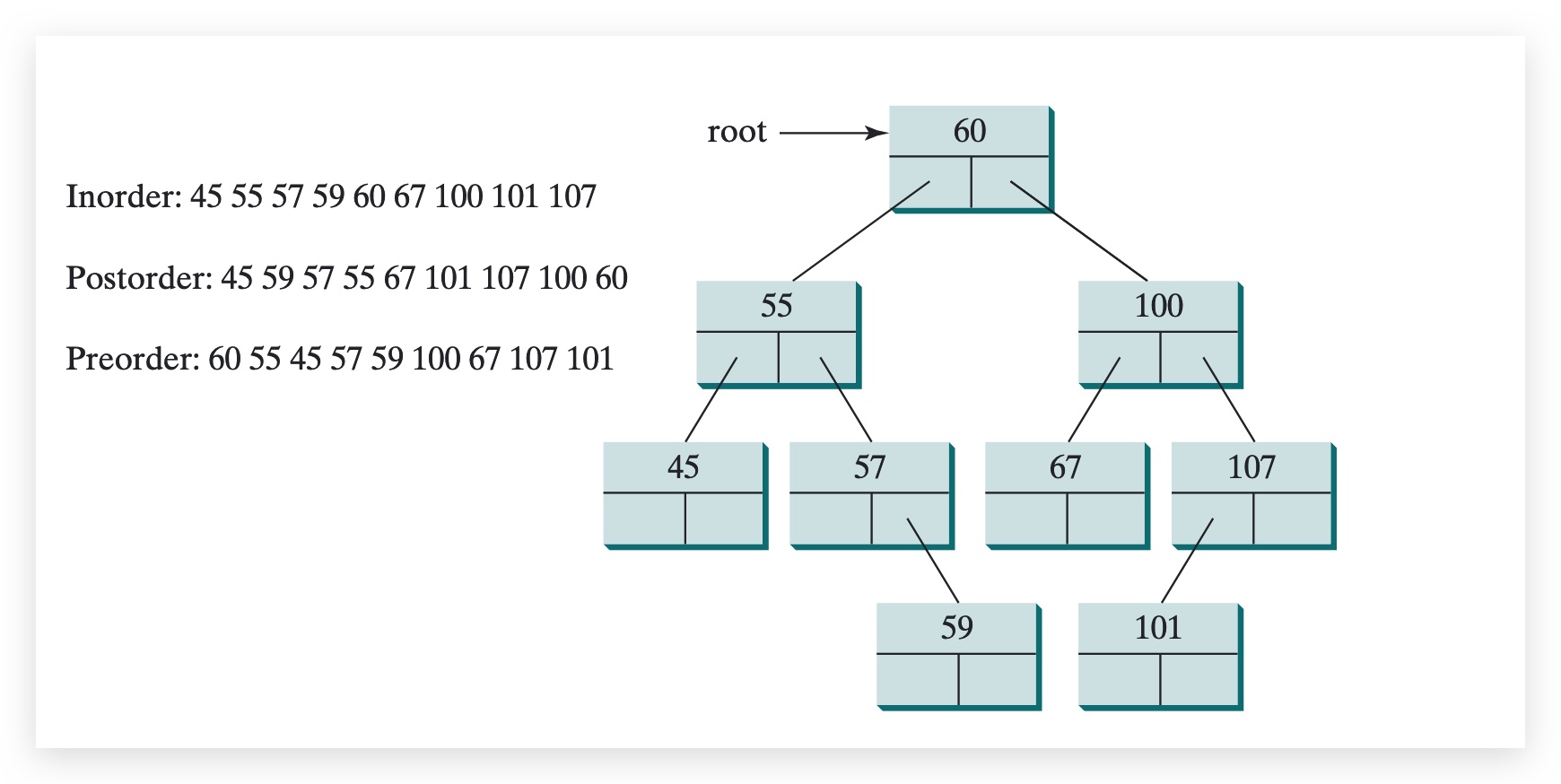
25.6 Tree Traversal

• inorder traversal
• postorder traversal
• preorder traversal